前几天,我在 Reddit 上面闲逛的时候,发现了一篇有趣的文章,名为《影响我们世界的十大算法》。作者 George Dvorsky 希望通过此文解释算法在当今世界上的重要意义,以及哪些算法为我们的文明做出突出贡献。
现在,如果大家对于算法有些涉猎,那么在读过文章后的第一个想法很可能是——作者真的知道算法是什么吗?或者说 Facebook 新闻源是否属于算法?因为如果 Facebook 新闻源也是一种算法,那么我们几乎可以把一切东西都归结为算法。因此,我希望在本篇文章中解释算法的真实定义,而后探讨 10 种(或者更多)真正支配着整个世界的算法。
算法究竟是什么?
直白地讲,算法是指一切经过明确定义的计算过程,其将某个或者某组值作为输入内容,并产生某个或者某组值作为输出结果。因此,算法代表的是一系列计算步骤,用于将输入转换为输出。——资源来源:Thomas H. Cormen 与 Chales E. Leiserson (2009 年),《算法导论》第 3 版。
更简单地总结,我们可以将算法视为一系列用于解决某个任务的步骤(是的,不仅仅是计算机会使用算法,人类同样在使用算法)。就目前的标准来看,算法应当具有以下三大重要特征才被视为拥有实际效果:
应该是有限的: 算法应该在有限的时间内用有限的步骤解决掉其旨在解决的问题,也就是说算法必须在有限的时间内可以完成,要不然就没有现实意义。
应该具有明确的指令: 算法中的每个步骤必须经过精确定义 ; 同时应针对每种情况做出明确说明。
应该切实有效: 算法应当能够解决其旨在解决的问题。此外,算法应该被证明可以单纯利用纸笔工具实现收敛。
此外,需要强调的是算法的应用不仅局限于计算科学,同时它也作为一种数学实体。事实上,早在公元前 1600 年就已经出现第一条记录在案的数学算法——巴比伦人发现了最早的已知算法,用于分解平方根。因此,回到文章开头我们讨论的问题,我读到的那篇文章将算法视为计算实体,但如果采取这样一个更为宽泛的定义,那么支配世界的十大算法很可能体现为算术方法(例如减法、乘法等)。
但是,如果采取我们在本文中做出的算法定义,那么问题仍然存在:支配世界的十种算法究竟有哪些?在这里,我列出一份小小的清单,排名不分先后。
1. 合并排序,快速排序与堆排序
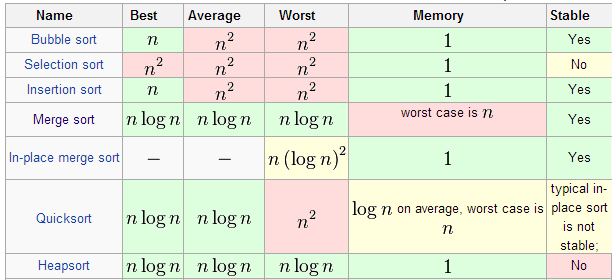
对元素进行排序的最佳算法是什么?具体答案取决于你的实际需要,因此我把这三种比较常用的排序算法列为同一类 ; 也许你更偏爱其中一种,但事实上三者都非常重要。
其中合并排序算法是迄今为止我们所拥有的最为重要的算法之一。这是一种基于比较的排序算法,以分治的方法解决原本时间复杂度为 O(n^2) 的问题。该算法由数学家 John von Neumann 于 1945 年发明得出。
快速排序是另一种用于解决排序问题的方法,其能够实现就地分区,同样属于一类分而治之的算法。该算法的问题在于其在排序方面并不稳定,但在对基于内存的数组进行排序时表现出色。
最后是堆排序算法,其利用优先级队列来减少数据中的搜索时间。该算法同样属于就地算法,且同样不属于稳定排序。
这些算法相较于我们之前使用过的其它方法(例如冒泡排序)有了很大的改进。事实上,正是由于这些算法的出现,我们才得以迎来数据挖掘、人工智能等网络上常见的众多现代计算工具。
2. 傅利叶变换与快速傅利叶变换

整个数字世界都在使用这些简单但非常强大的算法,这些算法能够将信号从时域转换为频域,反之亦然。事实上,正是由于这些算法的存在,本篇文章才能被更多朋友所看到。
互联网、Wi-Fi、智能手机、电话、计算机、路由器以及卫星等几乎一切具有内置计算装置的设备都会以这样或者那样的方式使用这些算法以保持运行。如果不研究这些重要的算法,大家也不可能拿下电子学、计算机或者通信科学学位。
3. 迪杰斯特拉算法(Dijkstra,又译戴克斯特拉算法)
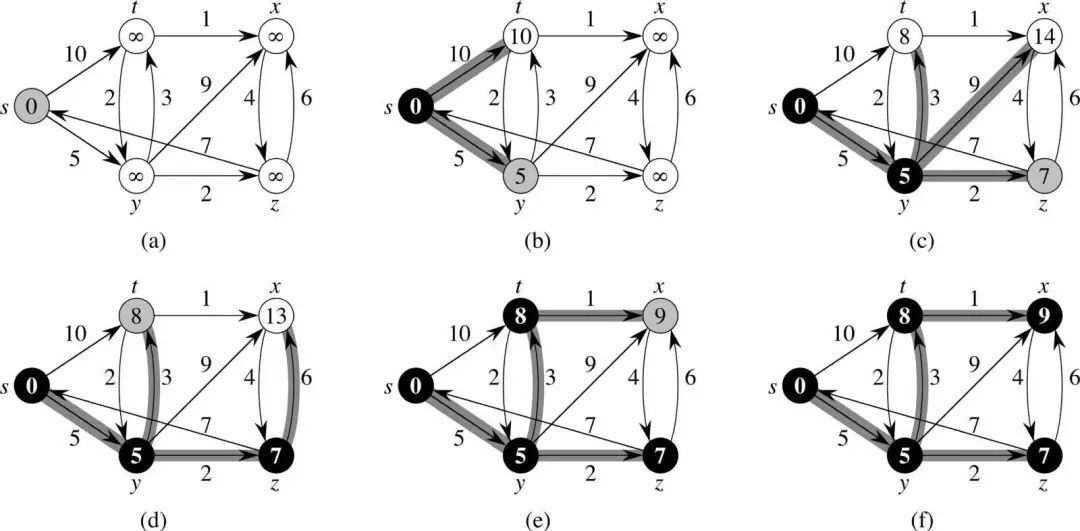
实事求是地讲,如果没有这种算法,互联网根本无法像今天这样保持高效运作。这种图搜索算法具有多种应用方式,能够将需要解决的问题建模为图,并在其中找到两个节点间的最短路径。
今天,虽然我们已经拥有更好的最短路径问题解决方案,但迪杰斯特拉算法仍然在强调稳定性的众多系统当中得到广泛应用。
4. RSA 算法
如果没有加密与网络安全机制作为保障,互联网的重要程度不可能达到如今的水平。大家可能会想“胡说,国家安全局局和众多情报机构的监控早就毁掉了互联网安全”或者“互联网根本就没有安全可言,傻子才会相信这种安全宣传”; 但必须承认,大多数人仍然具有一定程度的安全信心,否则你根本就不会通过互联网进行消费。毕竟如果真的否定现有网络体系的安全性,谁会愿意在 Web 服务中输入自己的信用卡号码?
在密码学领域,有一种算法仍然是目前世界上最重要的算法之一,这就是 RSA 算法。该算法由 RSA 公司的创始人们开发而成,使得密码学成果得以供世界上的每个人随意使用,甚至最终塑造了当今密码学技术的实现方式。RSA 算法希望解决的问题是如何在独立平台及最终用户之间共享公钥,从而实现加密(当然,我认为 RSA 算法并没能彻底解决这个问题,从业者们还需要在这个方向上投入更多努力)。
5. 安全哈希算法
这实际上并不是真正的算法,而是由 NIST(美国国家标准技术研究所)所开发的一系列加密散列函数。然而,该算法家族对于世界秩序的维持起到了至关重要的作用。从应用程序商店、电子邮件、防病毒软件再到常用的网络浏览器,这一切都在使用这类算法(实际上,使用的是由这类算法生成的哈希值),用以确定你所下载的是否正是你希望获得的内容,或者你是否已经成为中间人攻击或者网络钓鱼攻击的受害者。
6. 整数分解
这是一种在计算领域被大量采用的数学算法。如果没有这种算法,密码学技术的安全水平将受到严重破坏。该算法用于将复合数的质数因子分解为较小的非零因数。这也被称为 FNP 类问题,属于 NP 类问题的扩展,且解决难度极高。
很多加密协议都以分解大型复合整数或相关问题的难度为基础——RSA 算法就是其中的典型代表。正是由于对任意整数进行因子分解的难度极高,才使得基于 RSA 的公钥加密机制拥有较高的安全性水平。
量子计算的诞生大大降低了此类问题的解决难度,并开辟出一个全新的科学研究领域——利用量子特性保障系统安全。
7. 链接分析
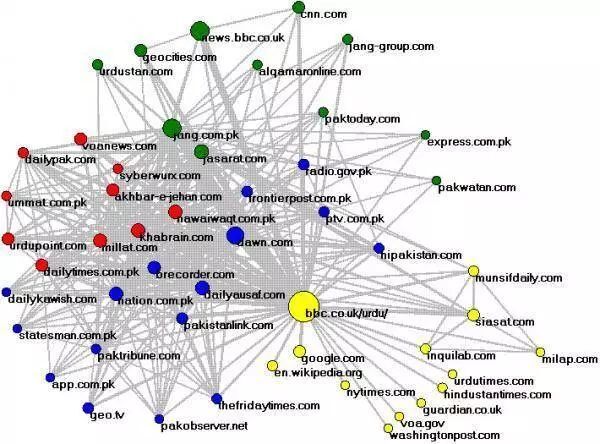
在互联网时代下,分析不同实体间的关系当然非常重要。从搜索引擎到社交网络再到营销分析工具,每一方都在努力发现随着时间推移而不断变化的互联网结构。
链接分析可以说是普罗大众眼中最神秘也最难以理解的算法之一。问题在于,我们可以通过多种不同方法实现链接分析,而且多种特征的存在使得每种算法间都存在着一定差异(允许对算法申请专利),但其底层基础却又高度相似。
链接分析背后的基本思路非常简单,即允许使用者以矩阵的形式表示图形,从而将其转化为特征值问题。这一特征值可以为我们提供衡量图形结构以及各节点相对重要性的好方法。该算法由 Gabriel Pinski 与 Francis Narin 于 1976 年发明得出。
那么,谁在使用这一算法?谷歌公司需要进行网页排名,Facebook 需要发布新闻提要(因此,我们将 Facebook 的新闻源服务视为算法结果,而非算法本身),Google+ 与 Facebook 的好友推荐,LinkedIn 的工作岗位与联系人推荐,Netflix 与 Hulu 的影视关联、YouTube 的相关视频等等皆属于这一类。虽然其各自拥有不同的目标与参数组合,但背后的数学原理却是相通的。
最后,我想强调一点,虽然很多人认为谷歌公司似乎是第一家使用这种算法的企业,但早在 1996 年(谷歌公司诞生的两年之前),由 Robin Li 开发的 RankDex 小型搜索引擎已经开始利用这一基本思路进行页面排名。最终,HyperSearch 的创始人 Massimo Marchiori 也开始使用这种基于单页间关系的页面排名算法。(谷歌在其申请的专利当中提到了这两位奠基者。)
8. 比例微积分算法
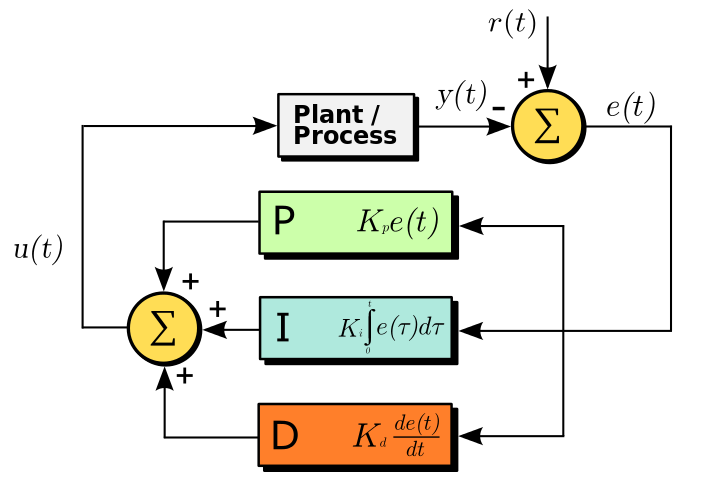
大家应该都体验过飞机、汽车、卫星服务或者手机网络吧?有些朋友还在工厂当中看到过机器人设备。如果是这样,那么你已经见识到了这一算法的威力。
该算法旨在利用控制回路反馈机制以最大程度控制期望输出信号与实际输出信号间的误差。其适用于一切存在信号处理需求的场景,包括以自动化方式通过电子技术控制的机械、液压或者热力系统。
也可以说,如果没有这种算法,那么我们的现代文明将无从谈起。
9. 数据压缩算法
很难确定哪种压缩算法的重要性最高,因为根据实际应用需求,大家使用的算法可能包括 zip、mp3 乃至 JPEG 以及 MPEG-2 等等。但相信大家都能清晰地感受到这些算法在各类结构中的重要作用。
除了最直观的文件压缩之外,大家还能在哪里看到压缩算法的踪影?很明显,网页会利用数据压缩技术控制你需要下载的文件体积,此外视频游戏、视频、音乐、数据存储、云计算以及数据库等也都是数据压缩算法大显身手的舞台。可以说,万事万物都离不开数据压缩,这类算法的存在使得系统能够以成本更低且效率更高的方式为用户服务。
10. 随机数生成算法

今天,我们还没有“真正的”随机数生成器,但已经拥有众多完全可以满足需求的伪随机数生成器。这些算法广泛存在于互连链接、加密、安全哈希算法、视频游戏、人工智能、优化、问题条件初始化以及财务等领域。
最后,我想补充一点:这份清单只代表一种观点,而非真正全面的列表。因为在机器学习、矩阵乘法以及分类等领域还存在着诸多堪称文明社会根基的重要算法,而我在本文中并没有明确提及。
